课程概况

课程性质

• 音乐基础理论课
• 通选课
• 导论课
• 学习曲线陡

成绩评定

• 平时作业5*4=20分
• 研究题30分
• 期末考试(闭卷笔试)50分

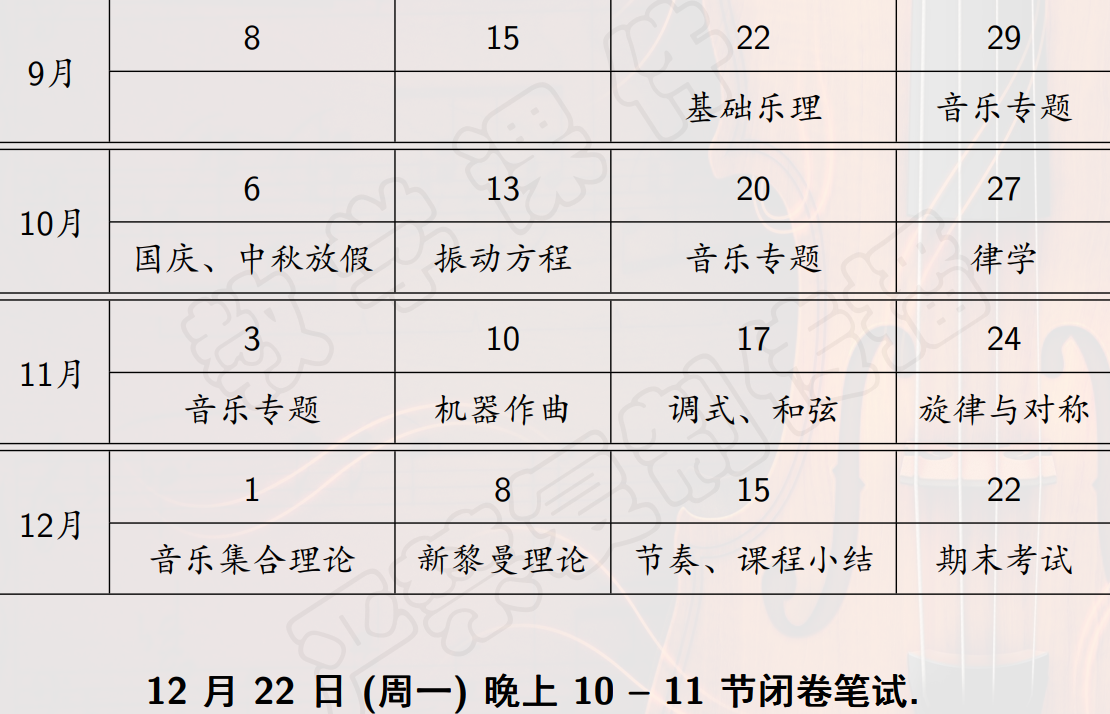
课程安排

节拍与节奏

节奏、旋律与和声是音乐的三大要素。 节奏与节拍是构成音乐的第一要素。 拍子是一段音乐中的基本律动。若干拍子按照一定的强弱规律组合形成节拍。

常见的组合拍子

• 二拍子
• 三拍子
• 四拍子
• 六拍子
• etc.

节拍

• 构成节拍的一组拍子循环出现，每次循环构成一个小节。乐谱中用小节线来标记一个小节的结束。
• 节拍通常用拍号来标示，比如2/4,3/4,4/4,6/8等。
• 例如2/4表示以四分音符为一拍，每小节有两拍。
• 二拍子、三拍子通常称为单拍子，由相同的单拍子结合而成的拍子称作复拍子。注意素数拍只能是单拍子。

节拍与节奏

• 节拍：若干拍子按照一定的强弱规律形成的组合
• 节奏：由音符的不同时值组合构成的模式。

固定节奏型

哈巴涅拉节奏型

• 忽略旋律变化，拍号为2/4
• 时值最短的是十六分休止符和十六分音符，一个小节分为八个时间单位（十六分音符）
• 抽象为没有音高的节奏型。

节奏的表示法

• 每个小格为一拍
• 标小圆点的为发声的起拍
• 空格为不发声的休止拍。
• 求出种类数：组合
• 固定节奏型：在乐曲无变化地反复出现，贯穿始终的节奏模式。

我们需要引入表示法和几何模型，以及若干关于节奏型的度量特征，以比较节奏型之间的异同:

节奏型的度量特征

• 极大均衡原则：在所有的拍上，要使起拍尽可能均匀分布。
• 节奏奇性：在节奏型的圆周表示中，将每个起拍对应的点，它的对径点都不是起拍。起拍点构成对径点的节奏型，起拍点被划分在两个等时值的半圆内，因此显得很有规律，通常包含偶数个起拍点的节奏型内会出现。节奏奇性使节奏呈现切分效果，增强节奏感与音乐的活力。
• 轮廓同构：节奏型的距离序列，是相邻起拍点之间的距离构成的序列。从古巴颂乐节奏型的距离序列中提取出特征，分别用$+,-,0$表示下一个距离比前一个增加，减少，保持不变。最后一个距离要与第一个距离作比较，这个序列称作颂乐节奏型的轮廓。如果$B$的轮廓序列可以通过循环移位得到$A$的轮廓序列，称节奏型$A,B$是轮廓同构的。
• 影子轮廓同构：将各个起拍之间的中点结合起来形成一个与发声的节奏型对偶的节奏，称为原来节奏型的影子。若影子与原来节奏型同构，则称为影子轮廓同构。注意影子节奏带的拍点位置不一定在原来节奏的拍点上。
• 相位：在乐曲中，由于固定节奏型持续不断地反复出现，故可以将其视为时间轴上的周期函数。同一个节奏型的不同表示缘于选取不同的起点（相位不同）。若两个节奏型可以通过旋转相互转换，则它们是同一个节奏型。古巴颂乐有$2-3$和$3-2$形式。它们是由前后两个小节调换位置得出来的，即$k \rightarrow k \oplus 8 \ \mathrm{mod} \ 16.$也就是相位上相同。

基于度量特征的结论

• 人们更容易注意到起拍与休止拍之间的交替变化，即相对变化；而对各拍的确切时值感受不敏感，即时间间隔的绝对长度。
• 于是，对于古巴颂乐，我们就可以得到$16$个符合极大均衡原则的节奏型。
• 古巴颂乐和$Fume-fume$的节奏型是轮廓同构的。
• 古巴颂乐是有唯一满足极大均衡原则、节奏奇性、影子轮廓同构的具有5个起拍的16拍节奏型。

音乐与数学

如果两个音的频率之比越接近于一个简单整数，那么这两个音听起来就越和谐。

和谐的音

• 纯八度
• 纯五度
• 纯四度
• 大三度
• 同度。