乐音体系的生成
- 乐音体系是有限多个音级组成的集合,这个集合中的元素是如何确定的?
- 这就是律学要解决的问题:
- 确定绝对音高,就是要确定每个音级对应的振动频率。
- 确定同一个八度内不同音级的相对音高。
- 一定意义上说,相对音高更为重要。
- 因为八度音程对应的频率比为$1:2$,如果同一个八度内的12个音级之间的频率比值确定,那么确定任意一个音级的振动频率,这个八度内其他音级的频率就随之确定。然后可以得到其他八度内各个音级对应的振动频率。
三分损益
- 在春秋时期《管子》一书"地员"篇中记载。
- 首先,计算初始值,即宫音,$3^4=81$。
- 对宫音增加三分之一,即徵音,$81 \times \frac{4}{3}=108$。
- 对徽音减少三分之一,即商音,$108 \times \frac{2}{3}=72$。
- 对商音增加三分之一,即羽音,$72 \times \frac{4}{3}=96$。
- 对羽音减少三分之一,即角音,$96 \times \frac{2}{3}=64$。
- 由于弦的长度与发声频率成反比,所以数字越大的音级频率越低,把徵音和羽音分别除以2,得到高八度的两个音级。
- 整理得到以下音列:
| (徵) | (羽) | 宫 | 商 | 角 | 徵 | 羽 |
|---|---|---|---|---|---|---|
| (108) | (96) | 81 | 72 | 64 | 54 | 48 |
-
假设宫音对应中央$C$,得到五声音阶$C,D,E,G,A$。

-
徵音与宫音的频率比为$4:3$,符合理想纯四度的简单整数比。
-
宫音与高八度的徵音频率比为$3:2$,符合理想纯五度的简单整数比。
-
但是宫音与角音的频率比为$81:64$,不符合理想大三度的简单整数比。
-
对角音继续做三分损益,得到变宫音$64 \times \frac{4}{3}=\frac{256}{3} \approx 85$和变徵音$\frac{256}{3} \times \frac{2}{3}=\frac{512}{9} \approx 87$。
-
整理得到新的音列
| (徵) | (羽) | (变宫) | 宫 | 商 | 角 | 变徵 | 徵 | 羽 | 变宫 |
|---|---|---|---|---|---|---|---|---|---|
| (108) | (96) | $\frac{256}{3}$ | 81 | 72 | 64 | $\frac{512}{9}$ | 54 | 48 | $\frac{128}{3}$ |
- 古代以清浊形容音的高低,
清宫就是比宫音高八度的音级,假设宫音为中央$C$,则三分损益法得到的七声音阶为

- 这就是传统音乐中的雅乐音阶,亦称为古音阶。
十二律
- 战国时期,《吕氏春秋》提出了十二律的名称和相生关系。
- 本质上是对七声音阶的拓展。

- 把十二律对应的数值从大到小(音高从低到高)排列,它与五音的联系如下:

- 得到$\sharp E$对应的数值后,继续做三分损益,得到它上方纯五度的$\sharp B$,其数值为$\frac{2^{17}}{3^7} \times \frac{2}{3}=\frac{2^{18}}{3^8}$
- 在现代律制中,$\sharp B$与高八度的$C’$等音,但实际上十二律会现代律制比略低,即旋宫不归。
五度相生
- 毕达哥拉斯假设中央$C$对应的频率为1,其上方五度的$G$对应的频率为$\frac{3}{2}$。
- 而$G$上方五度音的频率应该是$\frac{9}{4}>2$,超出同一个八度,因此降低一个八度,得到$D$对应的频率为$\frac{9}{8}$。
- 以此类推,产生全部十二个音名,完整的五度相生音阶。

- 纯五度和纯四度的音程频率都符合理想整数比,大三度频率,如$C \sim E$,其频率比为$\frac{81}{64} > \frac{5}{4}$,出现一定偏差。
- 得到音级$\sharp E$后,可以接着考虑其上方纯五度音的频率,$\frac{3^{11}}{2^{17}} \times \frac{3}{2}=\frac{3^{12}}{2^{18}}>2$。
- 将其降低八度,得到其频率为$\frac{3^{12}}{2^{19}} \approx 1.01 >1$。
- 按照现代律制,$\sharp E$上方五度应该是 $\sharp B$ ,降低八度后应该得到$C$,即上述式子应该等于1。
- 这就是著名的毕达哥拉斯音差。
- 单声音乐:单音曲调构成的音乐,包括没有伴奏的独唱、独奏,以及曲调作同度或八度重叠的齐唱、齐奏。
- 通常合唱比赛的都是齐唱,而非合唱,因为男女声部不算分声部。
- 多声部音乐:
- 公元9世纪前后出现奥尔加农音乐样式,是多声部音乐的雏形。
- 可以分为复调音乐和主调音乐。
- 复调音乐:不同声部具有各自的相对独立性,按照对位法结合在一起。
- 主调音乐:以一个声部为主要旋律声部,其余声部相对缺少独立性,对主要旋律起伴奏、烘托作用。
- 里切卡尔/无差部赋格:16-17世纪的一种复调器乐曲。
- 17世纪后出现了贯穿主题模仿的里切卡尔,结构近似赋格。
- 巴赫《音乐的奉献》中有一首六声部里切卡尔。
- 复调音乐如今不多见,常见的为主调音乐,如《军队进行曲》。
- 也可以在音乐中同时使用主调和复调,如贺绿汀《牧童短笛》。
纯律
- 文艺复兴开始,西方音乐越来越重视使用三度和六度音程。
- 纯律:在五度相生法中添加一个生律元素,理想大三度的比例 5:4,形成纯律。
- 据传为意大利音乐理论家扎利诺提出。
- 在纯律中, $E$ 的音高为 $\frac{5}{4}$,由于$E$和$B$形成纯五度,因此$B$的音高为 $\frac{15}{8}$。
- 又$F$和高音$C$构成纯五度音,因此$F$的音高为 $\frac{4}{3}$。
- 而$F$和$A$构成大三度音,因此$A$的音高为 $\frac{5}{3}$。
- 于是,正三和弦 $C-E-G,F-A-C’,G-B-D’$都符合理想整数比$4:5:6$,对于多声部音乐有重要意义。
- 纯律也有不足之处,即五度音程$D-A$不协和,其比例为$\frac{5}{3}:\frac{9}{8}=\frac{40}{27}<\frac{3}{2}$,比理想的纯五度窄。
- 同时,有两种不同的大二度(全音),音程$C-D,F-G,A-B$的比例为 $\frac{9}{8}$,而音程$D-E,G_A$的比例为 $\frac{10}{9}$。
- 存在音差(Comma)问题,从$C$出发升高4个纯五度,再降低两个八度和一个大三度,得到 $(\frac{3}{2})^4 \times (\frac{1}{2})^2 \times \frac{4}{5}=\frac{81}{80}$,即回到比$C$高一点的地方,这个数值被称为谐调音差(Syntonic Comma)。
- 存在转调问题。例如《保卫黄河》,《青花瓷》。
- 例如,对于$1=C$调好的音阶,要转为$1=D$,则其上方纯五度为$A$,其比例为 $\frac{5}{3} \times \frac{8}{9}=\frac{40}{27}<\frac{3}{2}$
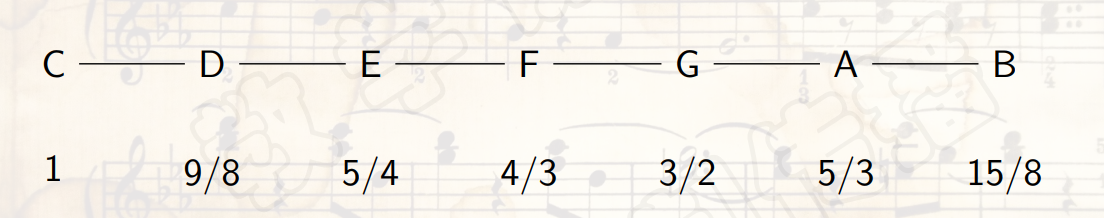
- 三分损益、五度相生和纯律都发挥过重要作用,但它们都存在缺陷。
- 我国出现过六十律、新律、三百六十律、十八律等律法。
中庸全音律
- 假定音名$C$的频率为$f$,则高八度$C’$的频率为$2f$,再高一个八度的$C’’$对应频率为 $4f$。
- 如果$C$上方五度的频率为 $\frac{3}{2}f$,则再高一个八度对应频率为 $(\frac{3}{2})^2 f$
- 经过 $n$ 次后,希望能有比 $C$ 高 $m$ 个八度的音级,对应频率满足 $(\frac{3}{2})^n \cdot f=2^m \cdot f$
- 即 $3^n=2^{m+n}$,易见不可能成立,即有理数范围内无法调好律。
- 回顾第一次数学危机,毕达哥拉斯学派是否认无理数的(他的学生希帕索斯发现无理数)。
- 于是,目标变为消除音差,通过牺牲纯五度的比例 $3:2$。
- 需要想办法将音差分配给不同的音级,新律实现了这种平均。
- 但是音程关系是频率的比值,对应于乘除而非加减,因此无法用算术平均解决问题。
- 假设 $a=\frac{81}{80}$ 为谐调音差,则其 $\frac{1}{4}$ 应该等于 $d=\sqrt[4]{a}$。
- 于是,得到缩小 $\frac{1}{4}$ 谐调音差后的纯五度音程比值为 $\frac{3}{2} \div \sqrt[4]{\frac{81}{80}}=\frac{3}{2} \times \frac{2\sqrt[4]{5}}{3}=\sqrt[4]{5}$ 。
- 再考虑 $F$ ,由于其上方五度的音级 $C’$ 与 $F$ 的比值应该等于生律元素 $\sqrt[4]{5}$,解得 $F$ 的音级为 $\frac{2\cdot 5^{\frac{3}{4}}}{5}$。
- 于是得到7个自然音级对应的数值:
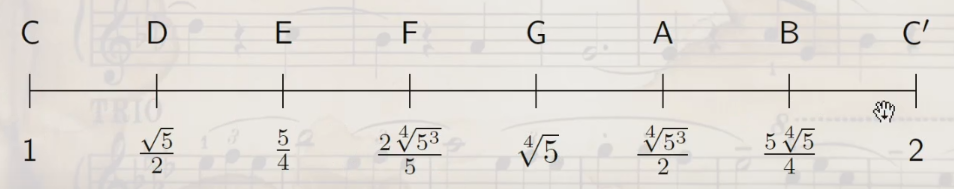
- 这就是中庸全音律。
- 有区分自然律和人工律,自然律就是泛音列,其音级都是有理数;而无理数一定是人工律。
- 纯律中有两种不同的大二度(全音),即 $C-D$ 和 $D-E$,它们的几何平均恰为中庸全音律中 $D$ 的值。
- 这说明了中庸全音律不仅保持了大三度音程的理想比例,又使得大二度音程的频率比相等。
- 计算小二度(半音) $B-C’$ 和 $E-F$ 的频率比,它们是相同的。但是两个小二度叠加,得到的频率比略大于一个全音。
- 中庸全音律消除了谐调音差,各个全音音程和各个半音音程一致,大小三度和大小六度都合于纯律,并且能在一定范围内转调,这是它的优点。
- 它牺牲了纯五度的理想比例,纯五度音程 $C-G$ 的比例等于 $\sqrt[4]{5}<\frac{3}{2}$,经过多次五度相生会产生与纯五度相差极大的五度音程,历史上称为狼五度。
平均律
- 设一个八度之间有12个半音,则相应的音级对应的频率构成一个等比数列,计算出其公比为 $r=\sqrt[12]{2}$,这就构成了十二平均律。
- 世界上第一个通过准确计算提出平均律的人是朱载堉,他把自己提出的平均律称为新法密率,并且精确到了小数点后25位。
- 巴赫的《音乐的奉献》基于"国王主题",包括两首无插入赋格,有一首是六声部的,还有十首卡农和一首以长笛为特色的三重奏奏鸣曲。
- 十首卡农中有一首"canon per tonos",意为"经由种种调性的卡农"。
- 它有三个声部,不断变调后又回到最初的 $C$ 小调。
音分
- 是度量不同声音的频率之比的单位,设两个声音的频率分别为 $f_1<f_2$ ,则两个声音之间的音分数是 $1200\log_{2} (\frac{f_2}{f_1})$。
- 对于平均律,则半音之间的音分是100音分。
- 同样,有音分可以求频率比, $r=2^{\frac{c}{1200}}$
- 将音级 $C$ 的频率记为 $f$,则 $G$ 的频率应该是 $2^{\frac{7}{12}} \approx 1.4983f$
- 普通人通常能分辨出 $4 \sim 6$ 音分的频率差。
- 对比平均律和纯律的音高,可以发现 $E$ 和 $A$ 分别高出了14音分和16音分,差距较大。
- 八度循环 $2:1$,五度纯正 $3:2$,和弦协和 $5:4$,这三个比例一直推动着人们进行不停探索,它们也被称为三条彩线。
- 上面提到的都是相对音高,历史上没有标准的绝对音高。
- 人们倾向于不断提高音高,主观上作曲家、演奏家和乐器制造者都追求用明亮、华丽的音色吸引听众,材料和制造技术的进步为提高绝对音高提供了客观可能性。
- 1939年国际标准化协会(ISA)确立 $A=440 \mathrm{Hz}$ 为音乐会音高。
- MIDI(Musical Instrument Digital Interface):乐器数字接口。
- 它用音符数 $21 \sim 108$ 代表 $A_0 \sim C_8$ 这88个音级。
- 若采用十二平均律和音乐会音高标准,则音符数 $n$ 对应的频率 $f$ 可以这样求出: $f=440 \cdot 2^{\frac{n-69}{12}}$
思考题
- 纯律中各自然音级之间的频率比能够唯一确定吗?
- 纯律中,各自然音级之间的频率比并不能唯一确定。例如 $A$ 的频率,我们先用高音 $C$ 推出 $F$ 的频率为 $4:3$,然后再通过大三度音得到 $A$ 的频率为 $5:3$。若通过 $D-A$ 构成纯五度音,推出 $A$ 的频率应该为 $27:16$。因此,纯律中的频率比并不唯一缺点。计算的方式不同,结果也不尽相同。
- 在纯律中,确定了各自然音级之间的频率比后,如何进一步确定变化音级的频率?
- 首先根据 $B$ 的频率 $15:8$ 推出 $\sharp F$ 的频率 $16:15$。
- 根据 $\sharp F$ 跟高八度的 $\sharp C$ 构成纯五度音,推出 $\sharp C$ 的频率 $16:15$。
- 根据 $\sharp C$ 和 $\sharp G$ 构成纯五度音,得到 $\sharp G$ 的频率 $8:5$。
- $\sharp G$ 和高八度的 $\sharp D$ 构成纯五度音,得到 $\sharp D$ 的频率 $6:5$。
- 最后根据 $\sharp D$ 和 $\sharp A$ 构成纯五度音,得到 $\sharp A$ 的频率为 $9:5$,这样得到了完整的七声音阶。
- 在实际演奏中,小提琴、二胡等弓弦乐器通常依照哪种律制确定其空弦的音高?
- 小提琴依据十二平均律确定,二胡依据五度相生确定。
声明
本笔记的部分内容来自喵喵的学习笔记 ,如有侵权请联系我删除。